Insights & Strategies: A Review of 2023 PSLE Math Paper 1

The PSLE Math paper is bro­ken down into Paper 1 and Paper 2. Although Paper 1 con­sists of only 1 or 2 mark ques­tions, it does not nec­es­sar­i­ly mean that they are eas­i­er than the ques­tions in Paper 2! We have seen our fair share of chal­leng­ing Paper 1 ques­tions that seem straight­for­ward at first glance, but actu­al­ly test stu­dents on their abil­i­ty to read between the lines. Stu­dents are also test­ed on their abil­i­ty to cal­cu­late quick­ly and accu­rate­ly since the use of a cal­cu­la­tor is pro­hib­it­ed for Paper 1. 

Let’s take a look at the trick­i­er ques­tions from the 2023 PSLE Math Paper 1. Most of these ques­tions test the student’s abil­i­ty to infer and solve. 

Question 7

This is a com­mon­ly test­ed ques­tion type that tests stu­dents on their abil­i­ty to com­pare frac­tions. If you noticed, the low­est com­mon mul­ti­ple of 12, 7, and 10 exceeds 100. Most stu­dents will see that a com­mon mul­ti­ple can be found by tak­ing 12 × 7 = 84, then mul­ti­ply­ing it by 10 to get 840. They might also take 7 × 10 = 70, then mul­ti­ply it by 12 to get 840. That would work, but they would get rather big num­bers. In fact, the low­est com­mon mul­ti­ple is not 840, but 420. 

Most stu­dents will make the denom­i­na­tors the same in order to com­pare frac­tions. Did you know that you can also make the numer­a­tors the same? In this case, find­ing the low­est com­mon mul­ti­ple of 3 and 7 is far eas­i­er than find­ing a com­mon mul­ti­ple of 7, 10, and 12.

If you were to make the numer­a­tors the same, the frac­tions will then become 21/36 , 21/49 , and  21/30 .  Will shar­ing 21 slices of cake with 49 peo­ple give you a big­ger por­tion, or will shar­ing 21 slices of cake with 30 peo­ple give you a big­ger por­tion? This will help us to see that 2130 is the biggest frac­tion, and 2149 is the small­est frac­tion. 

There­fore, option 4 is the cor­rect answer.

Question 13

For ques­tions that ask for “largest pos­si­ble num­ber” or “least num­ber of”, stu­dents have to note whether they should have a larg­er pro­por­tion of the high­er-val­ue item, or the small­est pro­por­tion of the high­er-val­ue item. In this case, we want the largest pos­si­ble NUMBER of coins, there­fore, we should have as few of the high­er-val­ue item (50-cent coin) as pos­si­ble so that we can have more 10-cent coins that make up the total.

Since there is a mix­ture of 50-cent and 10-cent coins, we can’t have 0 50-cent coins. There­fore, the min­i­mum num­ber of 50-cents will be one. If there is 1 × 50-cent coin, this means that the remain­ing $3 — $0.50 = $2.50 will be made up of 10-cent coins. Is it pos­si­ble to have 10-cent coins amount to $2.50? Yes, it is! 

$2.50 ÷ $0.10 = 25

There­fore, the largest pos­si­ble num­ber of coins in the box is 25 + 1 = 26.

Question 15

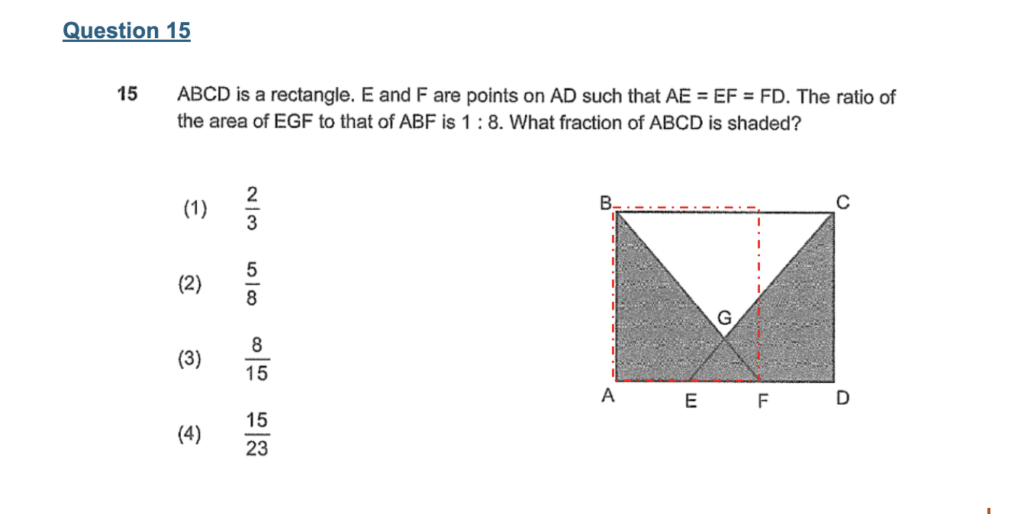
This is an inter­est­ing area and perime­ter ques­tion with no num­bers giv­en except for a ratio.
If you noticed, tri­an­gle EGF is part of tri­an­gle ABF. This means that the area of tri­an­gle ABF is
8 units and the area of tri­an­gle EGF is 1 unit. 

AE = EF = FD. This means that each of these lengths is 1 unit. 

Tri­an­gle ABF has a base of 2u and the rec­tan­gle that it is in has a base of 2u. (refer to red dot­ted box). 

Since Tri­an­gle ABF has an area of 8u, this means that the rec­tan­gle it is in will have an area that is twice of it, which means that the rec­tan­gle has an area of 16u. This rec­tan­gle has a base of 2u and the same height as ABCD, which has a base of 3u. This means that the red dot­ted box has an area that is 2/3 of rec­tan­gle ABCD. 

If 2/3 of rec­tan­gle ABCD is 16u, then the area of rec­tan­gle ABCD is 16u ÷ 2 × 3 = 24u.

The shad­ed por­tions have an area of 8u × 2 – 1u (over­lap­ping area of tri­an­gle EGF) = 15u.

This means that out of the 24u, 15u are shad­ed. 

15/24  = 5/8

The answer is there­fore 5/8 .

Question 24

This is a ques­tion that tests stu­dents on their infer­en­tial skills. Females are bro­ken up into 3 cat­e­gories – youth, adults, and senior cit­i­zens. If 50% of the females are adults, what does it say about female youths and female senior cit­i­zens? This means that they make up the oth­er 50% of the female mem­bers. 

There­fore, 50% of the females = 28 + 44 = 72

Part (b) can also be answered eas­i­ly once stu­dents recog­nise that the num­ber of male mem­bers remained the same, but the total decreased. This means that the male mem­bers will now take up a larg­er pro­por­tion of the mem­bers. There­fore, the per­cent­age of male mem­bers would have increased from June to July. 

Question 26

26(a) is pret­ty straight­for­ward. Out of 25 throws, Kalai’s ball passed through the hoop 20 times. This means that the ball did not pass through the hoop 5 times. 

For pass­ing through the hoop 20 times, Kalai would have scored 20 × 1 = 20.

For miss­ing the hoop 5 times, a total of 5 × 1 = 5 points would have been deduct­ed. 

There­fore, the final score from the first 25 throws would have been 20 – 5 = 15.

26(b) con­tin­ues from part (a).
Kalai con­tin­ues for anoth­er 5 more throws and end­ed up with an even­tu­al score of 18.
Did all 5 last throws have the ball pass through the hoop? No.
Had all the 5 balls passed through the hoop, Kalai would have scored an addi­tion­al 5 marks. How­ev­er, she only scored an addi­tion­al 3 marks. 

Since the num­bers are small, it will not be dif­fi­cult to do a lit­tle guess and check. How­ev­er, stu­dents at TTA have also been taught the Assump­tion method in the event that they are faced with larg­er num­bers in future. The Assump­tion method can be eas­i­ly applied by fol­low­ing the steps: Assume, Dif­fer­ence, Divide. 

Assume

Let’s start off by assum­ing that 5 of her throws passed through the hoop.

In that case, she would have scored 5 × 1 = 5 points.

Big Dif­fer­ence

We know from her final score that she only man­aged to earn an addi­tion­al 3 points. This means that there is a big dif­fer­ence of 5 – 3 = 2 points between the assumed total and the actu­al total. 

Small Dif­fer­ence

If we replaced a ball that passed through the hoop with a ball that did not, how many points will Kalai lose? 

1 + 1 = 2. Not only did Kalai fail to earn the 1 point, but she also got a point deduct­ed for miss­ing the hoop. 

Divide

How many times must we replace a ball that passed through the hoop with a ball that did not? 

2 ÷ 2 = 1. 

This means that out of the 5 throws, she missed 1 ball, and the oth­er 4 times, the ball passed through the hoop. 

The answer for 26(b) is there­fore 4. 

Question 27

This ques­tion involves a pro­mo­tion. Buy 10, get 2 more for free. 

There­fore, ques­tion 27 is a sets ques­tion type. 

The first 3 steps of a sets ques­tion type are the same: 

Big diff/total, Small diff/total, Num­ber of sets

The ques­tion gave us the big total of 120 eggs.
There­fore, we will focus on the small dif­fer­ence of a set. 

Big total -> 120 

Small total -> 12

No. of sets -> 120 ÷ 12 = 10

The ques­tion did not tell us how much she paid in total, but how much less she paid. This means that she would have to pay $4.80 more for every sin­gle one of the 120 eggs with­out get­ting any of them for free.

One set con­sists of 2 free eggs.
In 10 sets, there will be 10 × 2 = 20 free eggs. 

With­out the pro­mo­tion, Mrs Lim would have spent $4.80 more for the 20 eggs that she got for free as a result of the pro­mo­tion.

20 eggs –> $4.80 

10 eggs -> $2.40

Question 28

The tricky part about this ques­tion is fig­ur­ing out the addi­tion­al dis­tance Faizal jogged com­pared to Elise. When Faizal had reached point R, Elise had not reached point Q. As Faizal turned around and jogged towards Elise, they met at point Q. By this time, Faizal had jogged the addi­tion­al dis­tance of Q to R and from R to Q again.
This means that he jogged an addi­tion­al 600m × 2 = 1200m.

In a min, Faizal jogs 30m more than Elise. How long did it take him to jog 1200m more?

1200m ÷ 30m/min = 40min

Both Elise and Faizal had jogged for 40min before they met at point Q. 

In that 40min, Elise man­aged to cov­er a dis­tance of 4000m.
This means that her speed was 4000m ÷ 40min = 100m/min

That sums up the trick­i­er ques­tions in Paper 1. Keep an eye out for Paper 2 com­ing up in the fol­low­ing blog.

At Think Teach, our math lessons are designed to make learn­ing easy and enjoy­able, not stress­ful. We pro­vide chal­leng­ing ques­tions to push your child’s think­ing and help them mas­ter com­mon­ly encoun­tered prob­lems effort­less­ly. Our empha­sis on con­sis­ten­cy ensures that with struc­tured prob­lem-solv­ing tech­niques, every math ques­tion becomes famil­iar and man­age­able. Your child won’t see math as an insur­mount­able obsta­cle any­more. Remem­ber, prac­tice leads to per­fec­tion. If some­thing feels unfa­mil­iar at first, keep prac­tis­ing until it becomes sec­ond nature!

This arti­cle was proud­ly writ­ten for you by TTA’s Math Team. Our strat­e­gy in help­ing stu­dents achieve exam excel­lence is sim­ply to expose them to every type of ques­tion that could come out for PSLE and arm them with our easy-to-apply tech­niques and would help them approach these ques­tions sys­tem­at­i­cal­ly

For 2023 PSLE Math Paper 2