A Review of The 2022 PSLE Mathematics Paper

1. Dif­fi­cul­ty Lev­el: 7/10

The 2022 PSLE Math paper was chal­leng­ing in parts but over­all a man­age­able paper with lit­tle sur­pris­es. Unlike pre­vi­ous years, the 2022 paper includ­ed more syl­labus-based ques­tions and few­er ques­tions that were IQ-based and that which required think­ing out of the box.

 Let’s look at the trick­i­er ques­tions from 2022:

2. 2022 PSLE Math­e­mat­ics Paper 1 Book­let A: Rearrange and Form

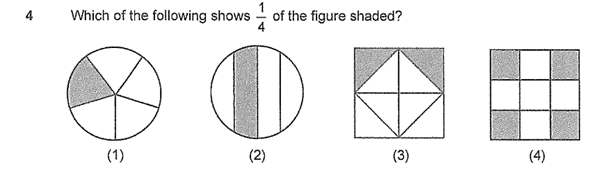
In order to get Ques­tion 4 right, we need to remem­ber that frac­tions mean EQUAL parts of the same whole. In option 2, although the cir­cle was divid­ed into 4 parts, they were not 4 EQUAL parts.
The cor­rect answer is there­fore option 3. Since there are 8 equal tri­an­gles, and 2 were shad­ed, it means that 2/8 of the fig­ure was shad­ed. 2/8 is equiv­a­lent to 1/4.

Anoth­er way would be to Rearrange and Form. By shift­ing the tri­an­gle over, the fig­ure is now divid­ed into 4 small­er squares, and of the 4 small­er squares, 1 of them is shad­ed. The Rearrange and Form tech­nique can be applied to more com­plex ques­tion types. Watch the video below to see how else it is applied!

3. 2022 PSLE Math­e­mat­ics Paper 1 Book­let A: Nets and Solids

Although Nets and Solids is not a major top­ic in the syl­labus, a ques­tion on nets and solids can be a stum­bling block espe­cial­ly for those who are less spa­tial­ly gift­ed. Fret not! With some tips and tricks, stu­dents can quick­ly iden­ti­fy which of the above is the net of a cube. If a net falls into a 1–4‑1, a 1–3‑2, a 2–2‑2, or a 3–3 net, then it can most cer­tain­ly be fold­ed along the lines to form a cube. 

4. 2022 PSLE Math­e­mat­ics Paper 1 Book­let A: Gaps and Sub­jects

In Ques­tion 14, a less com­mon­ly seen shape is featured—the hexa­gon. This ques­tion, how­ev­er, draws inspi­ra­tion from the Gaps & Sub­jects ques­tion type. To work your way around this ques­tion, first iden­ti­fy the dots on the fixed spots—the cor­ners.

Since a hexa­gon has 6 cor­ners, there will def­i­nite­ly be 6 dots in total for these 6 cor­ners.

Bear­ing in mind that the remain­ing dots are split equal­ly among the 6 sides, we have 18 – 6 = 12 dots to split among the 6 sides. 12 ÷ 6 = 2. We would then place 2 dots in between the cor­ners. 

This means that along one side of the hexa­gon, there will be the 2 dots in between, plus the 2 dots on the cor­ners, and that will leave us with 4 dots along one side. 

In a big­ger hexa­gon with 96 dots, there will still be 6 cor­ners. 

96 – 6 = 90 dots. This leaves us with 90 dots to split among the 6 equal sides. 

90 ÷ 6 = 15. 

Along one side of the hexa­gon, we will have 15 dots in between, plus the 2 dots on the cor­ners, and that will leave us with 17 dots along one side. 

5. 2022 PSLE Math­e­mat­ics Paper 1 Book­let A: Equat­ing Numer­a­tors

When­ev­er a frac­tion of A is equal to a frac­tion of B, this is an Equat­ing Numer­a­tors ques­tion type. In this ques­tion, 23 of A is equal to 78 of B. When you equate the numer­a­tors, you make them the same num­ber. The low­est com­mon mul­ti­ple of 2 and 7 is 14. There­fore, 1421 of A is equal to 1416 of B.

A is 21 units long with 14 units of it above the ground, and 7 units of it in the ground.

B is 16 units long with 14 units of it above the ground, and 2 units of it in the ground.

Since the length of A in the ground is 30cm longer than the length of B in the ground, this means that 7u – 2u = 30cm

5u → 30cm 

1u → 30cm ÷ 5 = 6cm 

21u + 16u = 37u 

37u → 6cm × 37 = 222cm 

The total length of sticks A and B is 222cm.

6. 2022 PSLE Math­e­mat­ics Paper 1 Book­let B: Tricky and Chal­leng­ing Ques­tions

Book­let B is rel­a­tive­ly easy. The fol­low­ing would be the 3 trick­i­est / most chal­leng­ing ques­tions of all the ques­tions in Book­let B.

Ques­tion 20 might cause care­less stu­dents to lose marks since the units of mea­sure­ment giv­en in the ques­tion were not the same. As the final answer is in kilo­grams, it would be wis­er to change 450g to kilo­grams, and work with that. 

Ques­tion 29 is a Sets ques­tion type. This is a lit­tle tricky since it is ask­ing for the GREATEST pos­si­ble num­ber of let­ters if there were 137 let­ter “A“s in the pat­tern. First, we’d iden­ti­fy the repeat­ing pat­tern, then pro­ceed to find out how many sets we would have.

There are 3 let­ter “A”s in a set. 45 sets would con­tain only 45 × 3 = 135 let­ter “A”s. There­fore, if we count for­ward 2 more “A”s, that would be our 137^th “A”. Since the ques­tion wants to know the max­i­mum num­ber of let­ters pos­si­ble with­out includ­ing the 138^th “A”, we will need to include the let­ter “C” that appears after the 137^th “A”.

If 1 set has 5 let­ters, 45 sets will have 45 × 5 = 225 let­ters. 

Since we’re includ­ing up till the let­ter “C” in the 46^th set, that would be an addi­tion­al 4 let­ters.
Hence, the great­est pos­si­ble num­ber would be 225 + 4 = 229 let­ters.  

Ques­tion 30 is what we would recog­nise as a Before-Change-After ques­tion type.

A Before-Change-After ques­tion type can be iden­ti­fied by pro­por­tion-change-pro­por­tion In the ques­tion. This par­tic­u­lar ques­tion involves 2 changes. Hence, the Before-Change-After table is length­ened to reflect 2 changes (B‑C-A-C‑A). 

We start off by writ­ing 9 under the num­ber of red beads and leav­ing the num­ber of blue beads blank. After adding a cer­tain num­ber (?) of red beads, the num­ber of blue beads became 25 of the beads. Hence, 2u for blue beads, and 3u for red beads. We can now fill in the “Before” stage for the blue beads as 2u since there was no change to the num­ber of blue beads.

Then, we add a col­umn for the yel­low beads. The change that occurred was an addi­tion of 56 yel­low beads. Remem­ber, the num­ber of blue beads remained the same through­out. There­fore, 2u are blue, 3u are red, and the remain­ing 9u – 2u – 3u = 4u must be yel­low beads. 

If the red beads start­ed off at 9, and end­ed up at 42, this would mean that 33 red beads were added. 

7. 2022 PSLE Math­e­mat­ics Paper 2: Mod­el Draw­ing

Mov­ing on to paper 2, it was man­age­able with no over­ly com­pli­cat­ed dia­grams for the geom­e­try, cir­cles, area and perime­ter, and pie chart ques­tion types. The bar graph and line graph in the data ques­tion types were not dif­fi­cult to read, and the ques­tions test­ed were straight­for­ward. 

Most of our stu­dents would have been con­di­tioned to draw­ing the Frac­tion-of-Frac­tion Mod­el (aka Drop-down Mod­el) once they see the phrase “frac­tion of the remain­ing” (high­light­ed in ques­tion). 

By using this mod­el tech­nique, our steps are kept short and sim­ple, leav­ing less room for care­less cal­cu­la­tion mis­takes and the loss of pre­cious marks. 

8. 2022 PSLE Math­e­mat­ics Paper 2: Simul­ta­ne­ous and Sub­sti­tu­tion

Ques­tion 13 might seem tricky at first, but it is a Simul­ta­ne­ous & Sub­sti­tu­tion ques­tion type that is sim­ply pre­sent­ed in a more visu­al way.

I would think that per­son who set this paper was very kind to have includ­ed Fig­ure 3. Look­ing at Fig­ure 3, one can clear­ly see that 2h and 1 side of the square = 58cm, and 3h + 2 sides of a square = 94cm. Based on these 2 equa­tions, we will then apply the Equate-Mul­ti­ply-Sub­tract tech­nique to solve this Simul­ta­ne­ous ques­tion type. For a deep­er under­stand­ing of this, watch the video on the Simul­ta­ne­ous and Sub­sti­tu­tion ques­tion type below. 

9. 2022 PSLE Math­e­mat­ics Paper 2: Frac­tions

Ques­tion 15 does seem a lit­tle out of the ordi­nary. Have you noticed it yet? Yes, there are no whole num­bers in this ques­tion at all! You sim­ply work with frac­tions with­out ever know­ing the cost of a file or how much Muthu had exact­ly. 

To start off, you would write down: 

6 pens → 4/7

1 pen → 4/7 ÷ 6 = 2/21

4 pens → 2/21 × 4 = 8/21

His remain­ing mon­ey was used on 4 pens and 3 files. If his remain­ing mon­ey was 37 of his mon­ey, and buy­ing 4 pens took up 821 of his mon­ey, this means that 3 files would cost him: 

3/7 — 8/21 = 1/21

Muthu spent 1/21 of his mon­ey on the 3 files.

1/21 of his mon­ey → 3 files 

There­fore, if he were to spend all of his mon­ey on files only, he would be able to get:

21/21 → 63 files

Since an addi­tion­al file was giv­en free for every 5 files he bought, this means that he would be able to get (63 ÷ 5 = 12 r 3) an addi­tion­al file 12 times!

63 + 12 = 75

With the good deal in place, Muthu would go home with 75 files.

10. 2022 PSLE Math­e­mat­ics Paper 2: Rearrange and Form 

This ques­tion makes use of the Rearrange, and Form tech­nique. 

Lines high­light­ed in blue are 12m each, lines in yel­low are 27m each, and the lines in pur­ple are the same length. 

Since these lines add up to 177m, and we know the lengths of the blue and yel­low lines, it is not dif­fi­cult to find the length of each pur­ple line (line AB). 

177m – (6 × 12m) – (2 × 27m) = 51m 

51m ÷ 2 = 25.5m

The length of AB is 25.5m. 

Part (b) is indeed more chal­leng­ing with a high­er weigh­tage of 3 marks. As with most ques­tions, infor­ma­tion in the ques­tion is rarely giv­en for the fun of it. Let’s make use of the area of 876m² to solve for the perime­ter. 

Since the fig­ure is made up of rec­tan­gles whose lengths and breadths we know, it is not dif­fi­cult to fig­ure out the area of the rec­tan­gle in the mid­dle. 

The rec­tan­gle on top has a length of 25.5m and a breadth of 12m, giv­ing it an area of 306m².

The rec­tan­gle at the bot­tom has a length of 27m and a breadth of 12m, giv­ing it an area of 324m².

There­fore, the rec­tan­gle in the mid­dle would have an area of
876m² - 306m² - 324m² = 246 m²    and   

a length of 246 m² ÷ 12m = 20.5m.

The fenc­ing took up 177m. To find the perime­ter of the plot of land, we’ll be exclud­ing the lines with­in the fig­ure. We now know that those lines are 20.5m each.

Hence, we can find the perime­ter by sim­ply tak­ing 177m – 20.5m – 20.5m = 136m

11. 2022 PSLE Math­e­mat­ics Paper 2: Num­ber x Val­ue

By pick­ing out the type of infor­ma­tion giv­en in the ques­tion, stu­dents will be able to iden­ti­fy this as a Num­ber × Val­ue ques­tion type. Most stu­dents will have no prob­lem with solv­ing for part (a). 

To solve part (b), we’ll make use of the Num­ber × Val­ue table. Since we only know the pro­por­tion of cher­ries (and not the exact num­bers) used for a large cake and a small cake is in the ratio of 3 : 2, we will use the units 3u and 2u to rep­re­sent the num­ber of cher­ries on each large and each small cake.

There­fore, 7 large cakes will have a total of 21u of cher­ries, and 15 small cakes will have a total of 30u of cher­ries. We can then eas­i­ly solve for the total num­ber of cher­ries used for all 15 small cakes, which is 30u.  

Each large cake requires 3u of cher­ries. Since 1u = 4, then 3u = 12.

Mrs Li has dec­o­rat­ed 7 large cakes. There are 25 large cakes so this means that she has 25 – 7 = 18 more large cakes to dec­o­rate. 

If each large cake requires 12 cher­ries, 18 large cakes will require 18 × 12 = 216 cher­ries. 

12. Con­clud­ing Remarks

We are pleased that the trick­i­er ques­tions in the PSLE 2022 Math­e­mat­ics paper involve heuris­tics con­cepts cov­ered in our cur­ricu­lum. Our 2022 batch of grad­u­ates were all well-equipped to tack­le the 2022 Math paper! Of course, Math is less about a stroke of good luck and more about being ana­lyt­i­cal in spot­ting exam trends or a shift in ques­tion types.

Over the years, we see shifts in trends and the evo­lu­tion of ques­tion types, and our cur­ricu­lum is updat­ed annu­al­ly to reflect the changes in the MOE syl­labus. We want to place our eggs in the right bas­kets, and have our stu­dents reap as much fruit from their labour. Our role as teach­ers is to help stu­dents con­nect the dots in the ques­tion and teach them how to make sense of infor­ma­tion in the ques­tion and solve it in the most time-effi­cient man­ner.

At Think Teach, Math lessons are struc­tured so that learn­ing is a breeze and not a tor­ture. Your child will be chal­lenged by tricky ques­tions and trained to solve com­mon­ly test­ed ones with ease. Con­sis­ten­cy is the key here to suc­cess. With a struc­tured approach to prob­lem-solv­ing, every Math ques­tion would seem famil­iar. Your child will no longer per­ceive every Math ques­tion as a daunt­ing moun­tain that he/she has not con­quered. As I like to say, “Prac­tice makes per­fect”. If some­thing at first seems unfa­mil­iar to you, keep on work­ing at it until you know it like the back of your hand!

After 3 years of being rav­aged by COVID, 2023 her­alds a change back to pre-COVID nor­mal. With stu­dents no longer con­sid­ered to be dis­rupt­ed by the pan­dem­ic, we are expect­ing PSLE to return to its full force – some­thing not seen since 2019. 

What does full force mean? First, there will be no reduc­tion of top­ics test­ed. Sec­ond, we expect PSLE papers will revert to their usu­al dif­fi­cul­ty lev­el from 2017 to 2019. Our teach­ers have found that the PSLE papers (not just Math­e­mat­ics but Eng­lish, Sci­ence, and Chi­nese) from 2020–2022 to be sig­nif­i­cant­ly eas­i­er than their pre­de­ces­sors. 

With 2023 being a year that gets us back to what life was like before COVID, can we expect PSLE to be more chal­leng­ing than 2022? We’ll find out togeth­er real­ly soon!      

This arti­cle was proud­ly writ­ten for you by TTA’s Math Team. Our strat­e­gy in help­ing stu­dents achieve exam excel­lence is sim­ply to expose them to every type of ques­tion that could come out for PSLE and arm them with our easy-to-apply tech­niques and would help them approach these ques­tions sys­tem­at­i­cal­ly